70. 爬楼梯

发表于 | 分类于 | 阅读次数：

链接：https://leetcode-cn.com/problems/climbing-stairs/

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。
示例 1：

1
2
3
4
5
输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

1
2
3
4
5
6
输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

分析

首先对于这一题的思考很流畅的能够想到递归，求解N解问题，实际上可以通过求解N-1阶问题和N-2阶问题。我们画出递归树：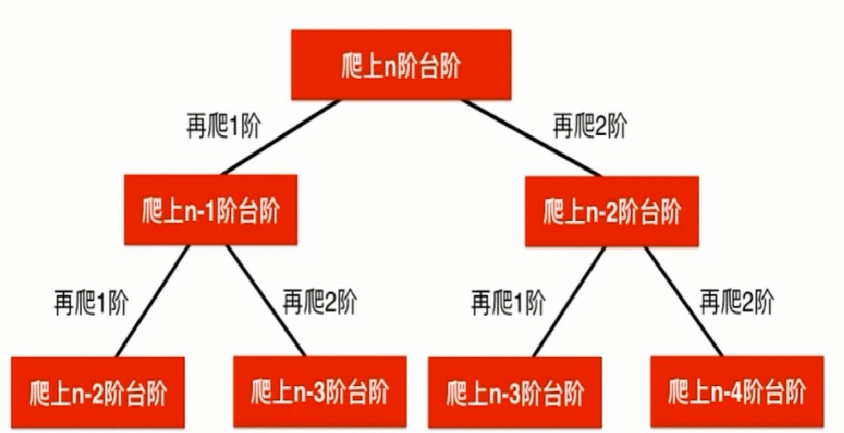
Alt text

从递归树里面我们也能看到很明显递归树中存在着大量的重叠子问题，所以要使用记忆化搜索进行缓存，当然既然能够使用记忆化搜索，这道题也就同时能够用动态规划的方法解决了。

答案

未记忆化搜索直接递归

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def climbStairs(self, n: int):
        return self.dfs(n)
        
    def dfs(self, n):
        if n == 1:
            return 1
        if n == 2:
            return 2
        
        return self.dfs(n - 1) + self.dfs(n - 2)

超时。
Alt text

记忆化搜索

稍作改变，使用一个列表缓存起来即可，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def __init__(self):
        self.solved = None

    def climbStairs(self, n: int):
        self.solved = [0] * n
        return self.dfs(n)

    def dfs(self, n):
        if n == 1:
            return 1
        if n == 2:
            return 2

        if self.solved[n - 1] == 0:
            self.solved[n - 1] = self.dfs(n - 1)
        if self.solved[n - 2] == 0:
            self.solved[n - 2] = self.dfs(n - 2)

        return self.solved[n - 1] + self.solved[n - 2]

可以看到效果还是不错的。
Alt text

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def __init__(self):
        self.solved = None

    def climbStairs(self, n: int):
        if n < 3:
            return n
        self.solved = [0] * (n + 1)
        self.solved[1] = 1
        self.solved[2] = 2
        for i in range(3, n + 1):
            self.solved[i] = self.solved[i - 1] + self.solved[i - 2]

        return self.solved[n]

可以很明显能够看出来，递归是先算n…..1,然后动态对话是先算1….n的，这就反应出了他们的不同的思路，即递归式自顶向下，动态规划是自底向上的。

能够看到，动态规划的效果还不错：
Alt text